1. ELECTRIC CHARGES AND FIELDS ( SHORT QUESTION ANSWER 2022 )
Q.1. An electric dipole is held in a uniform electric field.
(i) Using suitable diagram, show that it does not undergo any translatory motion and
(ii) Derive an expression for the torque acting on it and specify its direction.
Ans ⇒ Consider an electric dipole consisting of two equal and opposite charges +q and -q separated by a small distance 2a. If o be the angle the dipole makes with the electric field, then, the torque acting on the dipole is given by
(i) In the given diagram, the force on +q charge is +qE and

The force on – q charge is – qE.
Therefore, the net force on the system of charge at its centre is – qE + qE = 0
Hence, the translatory motion of the centre of charge will be zero.
(ii) Torque = Force x Perpendicular arm of the couple
t = F x AC.
t = F x AB sin θ
= qE x 2a sin θ
But, Dipole moment, p = q x 2a
Hence, t = pE sin θ
→ → →
In vector t = p x E
Q.2. What are the properties of electric charges ?
Ans ⇒ The following are the properties of electric charges :
(i) They are always additive in nature.
(ii) The charge is a scalar quantity.
(iii) The charge is of two types i.e., +ve and -ve.
(iv) The charge is always quantised.
(v) The charge of an isolated system always remains conserved.
(vi) The charge on an object unlike mass is not affected by the motion of the object.
(vii) Similar charges repel each other and unlike charges attract each other.
Q. 3. What is ∈0 ? Why it has been introduced ?
Ans ⇒ ∈0 is called as absolute permittivity of free space or vaccum of air. In most of the results developed from electrostatics, a factor 4π is obtained. These results are used for frequently than Coulomb’s law itself. To avoid the appearance of factor 4π, the proportionality constant k is defined as

= 8.854 x 10-12 C2 N-1 m-2.
Q.4. Explain the underlying principle of a parallel plate capacitor. If two similar plates, each of area A having surface charge densities +σ and -σ are separated by a distance in air, expression for
(i) the electric field at points between the two plates
(ii) the potential difference between the plates
(iii) the capacitance of the capacitor so formed.
Ans ⇒ To increase the capacitance of a conducting plate, an unchanged grounded conducting plate is brought near it. An opposite charge is induced on the grounded plate which reduces the potential of the first plate without bringing any change in its potential. This potential difference allows the conducting plates to have more and more charge.

Q. 5. State the superposition principle for electrostatic force on a charge due to a number of charges.
Ans ⇒ Superposition principle for electrostatic force on a charge due to number of charge states that the net force on the given charge is the vector sum of the individual forces exerted on the given charge by the other number of charges i.e.
![]()
where F1, F2, F3 …………… Fn are forces due to charges q1, q2, q3, ………. qn on given charge q.
Q.6. What is the cause of the origin of a fundamental force between charged particles ? Which basic law does govern this force ? Compare these aspects with a fundamental force between nucleons.
Ans ⇒ As per quantum theory, mainly exchange of photons responsible for a fundamental force between charged particles. This force is governed by inverse square law i.e.
![]()
where k is a constant, Q1 and Q2 are electric charges and r is the distance between the charges.
Similarly, as per quantum theory, mainly exchange of photons is responsible for a fundamental force between two nucleons.
This force i.e. nuclear force is governed by Yukawa force given by Fr = ϒe-r/ro
where ϒ and r0 are constants.
Q.7. It is now believed that protons and neutrons are themselves build called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge +(2/3)e, and the ‘down’ quark (denoted by d) of charge (-1/3)e, together with electrons build up ordinary matter. Suggest a possible quark composition of a proton and neutron on the basis of their charges.
Ans ⇒ ![]()
∴ Charge on proton = +e
Since it is made of 3 quarks, therefore, composition of proton can be
![]()
i.e. udd = 0 charge on neutron.
Q.8. What is electric flux ? Write its SI units. Using Gauss’s theorem, deduce an expression for the electric field at a point due to a uniformly charged infinite plane sheet.
Ans ⇒ Electric flux through an area is defined as the total number of electric lines of force passing through the area normally and is given by
→
φ = EA cosθ = E.A
Its SI unit is Nm2/C.
Gauss’s theorem : According to Gauss’s theorem, the total electric flux through closed surface is equal to 1/∈0 times the total charged enclosed by the surface.
![]()
SEO Consider an infinite plane sheet of charge having surface charge density σ. Let B be a point at a distance r from it. Let us consider a Gaussian surface in the form of a cylinder of length 2l and area of cross-section A arranged such that its lateral surface is parallel to the field lines and its ends are normal to the field lines as shown in Fig.

Q.9. Using Gauss’s Theorem, show mathematically that for any point outside the shell, the field due to a uniformly charged thin spherical shell is the same as if the entire charge of the shell is concentrated at the centre. Why do you expect the electric field inside the shell to be zero according to this theorem ?
Ans ⇒ Consider uniformly charged thin spherical shell. Let the total charge on the shell be A. To calculate electric field at a point outside the shell, we consider a symmetrical Gaussian surface around the shell in such a way that the observation point lies on it shown in Fig.
Electric flux through gaussian surface
= E. 4πr2 … (1)
Electric flux = Q/∈0 …(2)
∴ E. 4πr2 = Q/∈0

which is same as due to point charge of magnitude Q, located at the centre of shell.
For any point inside the shell, charge enclosed by Gaussian surface is zero. Hence, electric field is zero at any point inside the shell.
Q. 10. A charge q is placed at the centre of the line joining two equal charges Q. Show that the system of three charges will be in equilibrium if q = -Q/4.
Ans ⇒ System will be in equilibrium, if
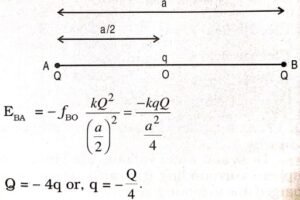
Q. 11. Check that the ratio ke2/G me mp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify ?
Ans ⇒

The ratio is the ratio of the force of electrostatic attraction and the gravitational force of attraction between a proton and an electron placed at the same distance apart.
Q.12. (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges ?
Ans ⇒ (a) The charge on a body is an integral multiple of the charge on an electron or proton (fundamental charge) i.e., q = ±ne, where n is an integer. This fact is called quantization of charge.
(b) At macroscopic level, we deal with charges that are enormous compared to the magnitude of minimum charge i.e., e (1.6 x 10-19 C). At this large scale if we say that charge increases or decreases in units of e is more or less saying that charge takes continuous value and its quantisation is insignificant and can be ignored.
Q.13. (a) An electrostatic field line is a continuous curve. That is a field line cannot have the sudden breaks. Why not ?
(b) Explain why two field lines never cross each other at any point ?
Ans ⇒ (a) An electric line of force is continuous curve and it can not have sudden breaks because these will indicate the absence of electric field at break points.
(b) The electric lines of force give the direction of the electric field. In case, two lines of force intersect, there will be two directions of the electric field at the point of intersection, which is not possible.
Q.14. Derive an expression for the electric intensity due to a uniformly charged shell at a point (i) inside the shell and (ii) outside the shell.
Ans ⇒ Let us consider a shell of a radius R and centre 0. Let is be given a charge q. It will get distributed uniformly upon it. (fig.).
Imagine a point P such that OP = r. It is a Gaussian surface at every point of which electric

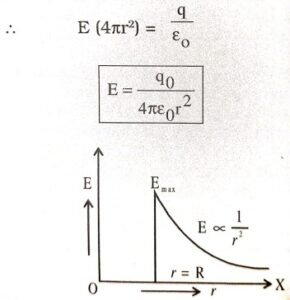
It is clear that electric intensity at any point outside the shell is such that the entire charge were supposed to be concentrated at the centre of the shell.
At point on the shell

If P lies inside the spherical shell, then r < R. Since charge inside the spherical shell is zero,
∴ q = 0 and hence E = 0
Electric intensity inside the spherical shell is always zero. Variation of E with distance from uniformly charged spherical shell is shown in the graph (Fig.)
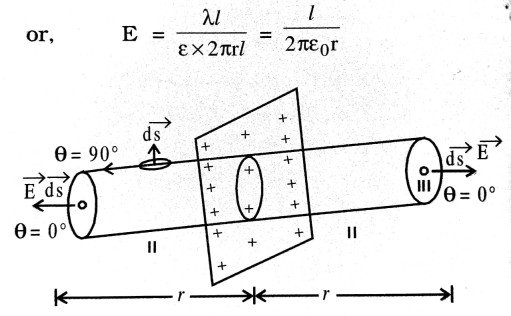
Q.15. Using the Gauss’s theorem, derive an expression for the electric field intensity due to an infinitely long straight wire of linear charge density λ C/m.
Ans ⇒ Let AB be a line charge having a linear charge density. Draw a Gaussian surface from the point P where we want to calculate the field say a cylinder with AB as the axis of the cylinder (Fig.). The flux through the cylinder is from the curved surface only, and in flux through the end faces is zero, because they are at 90° to field and the curved surface is in the direction of the field.
![]()
Q.16. (i) Write down unit and dimension of permittivity of free space.
(ii) A Gaussian surface contains three charges (-q), (+2q) and (-q). Evaluate net electric flux through the surface.
Ans ⇒ (i) S.I. unit of permittivity of free space is = C2N-1m2
Dimension = [M-1L-3T4A2)
(ii) Total charge inside the Gaussian surface
Q = (-q) + (+2q) + (-q) = 0
∴ Electric field E = 0
→ →
∴ Electric field φ = E . S
→
= 0.S
= 0 (zero)
Q.17. Atmosphere is not electrically neutral. Explain why ?
Ans ⇒ Dust and water vapours are present in the atmosphere surrounding the earth. These particles are charged due to induction of the negatively charged earth. That is why the atmosphere is not electrically neutral.
Class 12th physics Subjective question in English
| S.N | Physics Short Type Question English Medium |
| 1. | ELECTRIC CHARGES AND FIELDS |
| 2. | LECTROSTATIC POTENTIAL AND CAPACITANCE |
| 3. | CURRENT ELECTRICITY |
| 4. | MOVING CHARGES AND MAGNETISM |
| 5. | MAGNETISM AND MATTER |
| 6. | ELECTROMAGNETIC INDUCTION |
| 7. | ALTERNATING CURRENT |
| 8. | ELECTROMAGNETIC WAVES |
| 9. | RAY OPTICS AND OPTICAL INSTRUMENTS |
| 10. | WAVE OPTICS |
| 11. | DUAL NATURE OF MATTER AND RADIATION |
| 12. | ATOMS |
| 13. | NUCLEI |
| 14. | SEMI CONDUCTOR ELECTRONICS |
| 15. | COMMUNICATION SYSTEMS |
